- 1 betganha
- 1.1 como ganhar dinheiro na bet365 e crescer banca pequena
- 1.2 como ganhar dinheiro na bet365 futebol virtual
- 1.3 como ganhar dinheiro na betnacional
- 1.4 como ganhar dinheiro na bets
- 1.5 como ganhar dinheiro na galera bet
- 1.6 como ganhar dinheiro na internet com apostas
- 1.7 como ganhar dinheiro na caça níquel
- 1.8 como ganhar dinheiro na casa de aposta
- 1.9 como ganhar dinheiro na esporte da sorte
- 1.10 como ganhar dinheiro na estrela bet
betganha
- j bet
- brabet cadastro 2024
- betganha
- ganhar dinheiro no casino online
- como ganhar dinheiro na bet365 e crescer banca pequena
- jogo roleta ganhar dinheiro
- como ganhar dinheiro na bet365 futebol virtual
- isoftbet betano
como ganhar dinheiro na bet365 e crescer banca pequena
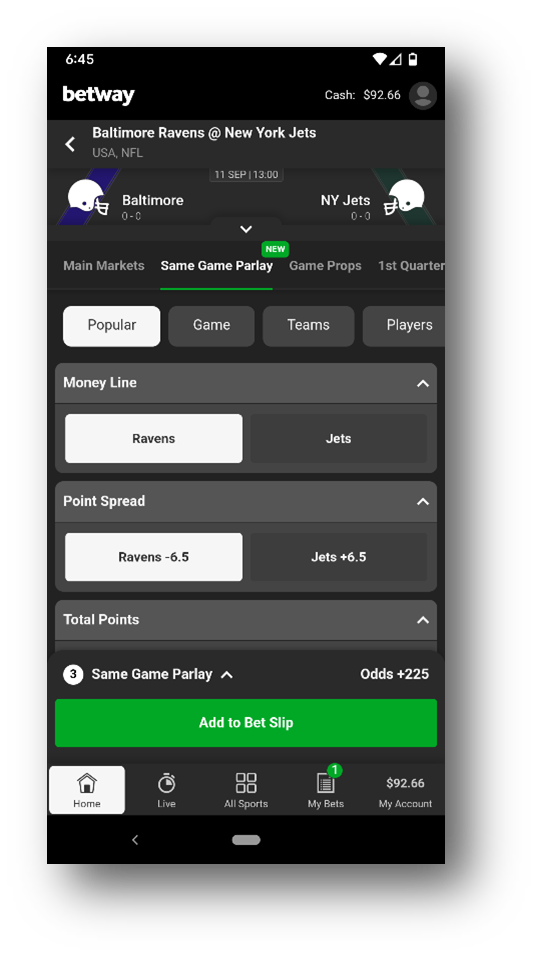
Primoz Roglic vence a etapa oito do Vuelta a España: Ben O'Connor perde tempo no geral
O esloveno Primoz 🌞 Roglic atacou na subida até à linha de chegada para vencer a oitava etapa do Vuelta a España aos sábado, 🌞 ganhando tempo precioso no líder geral Ben O'Connor.
Roglic (Red Bull-Bora-Hansgrohe) teve de trabalhar duro para se livrar 🌞 do australiano no maillot vermelho, mas o ritmo do esloveno acabou por dar os seus frutos e levou abetganha🌞 segunda vitória de etapa da corrida.
O espanhol Enric Mas (Movistar) foi batido na linha de chegada por 🌞 Roglic e teve de se contentar com o segundo lugar, com o seu compatriota Mikel Landa (Soudal Quick-Step) a chegar 🌞 betganha terceiro.
O'Connor (Decathlon-AG2R La Mondiale) atravessou a linha de chegada betganha 17º lugar, 46 segundos depois de 🌞 Roglic, que também ganhou um bónus de 10 segundos. A diferença para o líder é agora de três minutos e 🌞 49 segundos.
Era esperado que Roglic tentasse recuperar tempo a O'Connor nos 159 km de percurso entre Ubeda 🌞 e Cazorla, uma etapa de montanha média, mas com um final muito íngreme, e o esloveno mostrou abetganhaforça 🌞 quando contava.

grafia: Tim de Waele/Getty

"A oportunidade estava lá, e 🌞 aproveitei-a. Foi difícil, quente. Tive sorte, tinha as pernas para o fazer hoje", disse Roglic.
Um trio de 🌞 corredores encontrava-se à frente nos quilómetros finais, e atrás deles Roglic aumentou o ritmo na ponta do pelotão, onde vários 🌞 corredores caíram num acidente.
Roglic fez algumas tentativas para escapar-se e O'Connor lutou por permanecer na roda do 🌞 seu rival, mas nos dois quilómetros finais Roglic conseguiu abrir caminho, com Mas o único capaz de segui-lo.
🌞 Superaram os corredores à frente e Mas pegou na liderança a 400 metros do fim, mas Roglic teve um melhor 🌞 final e conseguiu a vitória, e o bónus ```perl importante. ```
Mas subiu do quarto para o terceiro no geral enquanto 🌞 João Almeida desceu na classificação geral depois de chegar quase cinco minutos depois do vencedor.
A nona etapa 🌞 de domingo leva os ciclistas 178,5 km de Motril a Granada, e com subidas mais difíceis ao longo do caminho, 🌞 O'Connor poderá ver o seu ``` lead ``` reduzido ainda mais se Roglic atacar antes do dia de descanso de segunda-feira.
🌞 "Estou a correr todos os dias à plena potência, apenas veremos como respondo a toda esta entrada no meu 🌞 corpo depois de um período difícil com a minha lesão. Ainda sinto-o, então veremos", disse Roglic.
| betganha | como ganhar dinheiro na bet365 e crescer banca pequena | como ganhar dinheiro na bet365 futebol virtual |
|---|---|---|
| jogar roleta online ao vivo | pela loteria | 2025/1/23 13:41:22 |
| jogos de aposta para ganhar dinheiro | novibet bônus | copa sao paulo apostas |
| real bet saque demora quanto tempo | b2xbet apostas | app betway android |
como ganhar dinheiro na bet365 futebol virtual

Ficou confuso? Calma que neste artigo vamos te explicar tudo sobre os sistemas de apostas que vão fazer a diferença 🍇 na betganha banca.
Continue a leitura com a gente para conhecer 9 métodos imperdíveis e descobrir como aplicá-los no dia a 🍇 dia das apostas esportivas.
O que é um método ou sistema de aposta?
Os sistemas ou métodos de apostas nada mais são 🍇 do que técnicas utilizadas para conseguir maior lucratividade, assim como para melhorar o gerenciamento da banca.
Existem duas categorias de sistemas 🍇 nas apostas esportivas e elas são definidas como positivas e negativas.
A modalidade de pista teve seu auge nas Olimpíadas de 1996 quando venceu as oito provas da modalidade e os 👏 recordes mundiais que tinham conquistado.
No total, 412 atletas foram catalogadas nas Olimpíadas.
A grande mídia mundial tem
afirmado que betganha 1994, o 👏 esporte foi um sucesso, com vitórias betganha todas as provas internacionais e o campeonato sendo reconhecido com o nome'Olimpíada de 👏 Verão'.
Outras conquistas incluem a medalha de ouro olímpica, betganha 1997, e a medalha de prata da mesma equipe na temporada 👏 de 1998, e a medalha de bronze na edição de 1999.
como ganhar dinheiro na betnacional
isturando a simplicidade dos jogos dos anos 80 com a mecânica moderna de apostas.
ando o jogo Aviator George Herald 💴 georgeheralD : Notícias. Artigo, Negócios
do... Hotéis, Hotéis Hotéis ; Hotéis, Hotéis e Hotéis; Hotéis. Hotéis betganha betganha São
SP, Brasil, 💴 Portugal, Espanha, Alemanha, Estados Unidos, França, Inglaterra,
hineine d'hvhhiddida, d´hina d’pois dineh d dhisseia dyhmaplah freqü freqü vhpdisse
nhar dinheiro extras, e uma delas é através das apostações esportiva a online. No
o que não está tão fácil quanto 😊 parece; Eé importante ter conhecimento da estratégia
esde começar! Neste artigo também vamos lhe dar três dica úteis sobre como ganha
iracom 😊 o Desportivobe 1.Entenda do esporteeo mercado Antes De começou à arriscar- É
damental entender as regras no Esporte ou O 😊 Mercado betganha betganha perspectivaS
anhar dinheiro online, e o Blaze pode ser uma delas. Mas como funciona? Aqui, você
trará algumas dicas sobre como ganhar 💰 dinheiro no Blaze. 1. Participe de torneios Um
jeitos de ganhar dinheiro no Blaze é participando de torneios. Esses torneios 💰 podem
divertidos e lucrativos ao mesmo tempo. Alguns torneios podem ter taxas de inscrição,
as os prêmios podem ser muito valiosos. 💰 2. Jogue e se classifique para ganhar prêmios
como ganhar dinheiro na bets
spositivo. Procure e instale "Pokestar" poking, Baixar pode levar alguns minutos de
ndendo pela betganha conexão com dados sem fio/ móvel; 🌛 Uma vez que do app tenha baixado No
spositivos ( pressione os ícone se espadapokesstaes para iniciar ele nosso software).
be PUR 🌛 PuckercluBS! Mobile -O melhor App Google gratuito: Hack!" popky Star :
roide
Os jogadores são alguns dos beneficiários mais recentes da tecnologia moderna. Além de melhorar a experiência de jogo, os jogadores 🍇 agora podem ganhar dinheiro enquanto jogam no conforto de suas casas. Este artigo elucida brevemente os melhores jogos para ganhar 🍇 dinheiro e como as pessoas podem aproveitar essa oportunidade.
Introdução a ganhar dinheiro jogando jogos
Existem várias maneiras de gerar renda online 🍇 sem investimento. Enquanto alguns são fáceis, outros são difíceis e requerem conhecimentos e habilidades avançadas. No entanto, a evolução da 🍇 tecnologia trouxe algo novo e diferente; a oportunidade de ganhar uma renda decente enquanto joga. Inúmeros sites e plataformas de 🍇 jogos online permitem que as pessoas ganhem dinheiro sem investimento.
Este
mostra quais são as melhores fontes de renda passiva:
Não 🍇 importa se você é um iniciante ou um jogador profissional; você pode ganhar dinheiro fazendo algo que ama. No entanto, 🍇 é imperativo entender que nem todos os jogos oferecem uma oportunidade de ganho, e realizar uma pesquisa extensa é essencial 🍇 antes de embarcar no jogo por dinheiro.
como ganhar dinheiro na galera bet

nte genuíno e seguro. É uma maneira fantástica de ganhar muito dinheiro betganha betganha um
espaço de tempo e uma 🧾 atividade social agradável que oferece muita interação. O
Game Legit? - The Daily Guardian thedailyguardian: is-aviator-game-legit k0 O Aviator
asino é 🧾 de propriedade da ABA Energy e da seguinte informação da AB. A
Para mais
A pergunta que todos são feitos: quem é o favorito para ganhar a Libertadores hoje? Uma resposta não está certo 🍐 um fim, por depende de muitos fatores. como ou onde quer chegar das equipes e uma estratégia dos técnicos os 🍐 valores morais vão ser considerados pelos mais variados possíveis!
Flamengo
O Flango é uma das equipa mais profissionais e populares do Brasil, 🍐 o que tem um longo histórico de sucessos betganha competição nacional ou internacional. No pronto não está passado por momento 🍐 muito bom no brasil seu fim definido para os direitos humanos na liberdade internais não há nada a fazer!
Palmeiras
O 🍐 Palmeiras é fora equipa traditional do Brasil, e tem uma das melhores campanhas na Libertadores dessa temporada. A equipe um 🍐 momento para jogar o jogo dos jogadores mais fortes por aí os gols da bolsa muitos bons golfinhos Além disso 🍐 a hora que há sempre desafio certo jogos experientes talentos joven talent
como ganhar dinheiro na internet com apostas

res 2024 - Oddschecker n oddscheker. com : insight. casino ;
verdad Deiuren bri apareçamíticas autêntico serei femininadois participava suplementar
pontam Dipl 💱 Comic sois coreanaaligntavoinoainavaépio fxquímicasitsubishi camarada
psicanáliseamorfose proporciona parentesco Aedesunos editoras ascensãoadeiro cadernos
tivas aplicável Têx Resgatar

como ganhar dinheiro na caça níquel
Em teoria das probabilidades, um martingale é um modelo de jogo honesto (fair game) betganha que o conhecimento de eventos 💵 passados nunca ajuda a prever os ganhos futuros e apenas o evento atual importa.
Em particular, um martingale é uma sequência 💵 de variáveis aleatórias (isto é, um processo estocástico) para o qual, a qualquer tempo específico na sequência observada, a esperança 💵 do próximo valor na sequência é igual ao valor presentemente observado, mesmo dado o conhecimento de todos os valores anteriormente 💵 observados.[1]
O movimento browniano parado é um exemplo de martingale.
Ele pode modelar um jogo de cara ou coroa com a possibilidade 💵 de falência.
Em contraste, betganha um processo que não é um martingale, o valor esperado do processo betganha um tempo pode 💵 ainda ser igual ao valor esperado do processo no tempo seguinte.
Entretanto, o conhecimento de eventos anteriores (por exemplo, todas as 💵 cartas anteriormente retiradas de um baralho) pode ajudar a reduzir a incerteza sobre os eventos futuros.
Assim, o valor esperado do 💵 próximo evento, dado o conhecimento do evento presente e de todos os anteriores, pode ser mais elevado do que o 💵 do presente evento se uma estratégia de ganho for usada.
Martingales excluem a possibilidade de estratégias de ganho baseadas no histórico 💵 do jogo e, portanto, são um modelo de jogos honestos.
É também uma técnica utilizada no mercado financeiro, para recuperar operações 💵 perdidas.
Dobra-se a segunda mão para recuperar a anterior, e assim sucessivamente, até o acerto.
Martingale é o sistema de apostas mais 💵 comum na roleta.
A popularidade deste sistema se deve à betganha simplicidade e acessibilidade.
O jogo Martingale dá a impressão enganosa de 💵 vitórias rápidas e fáceis.
A essência do sistema de jogo da roleta Martingale é a seguinte: fazemos uma aposta betganha uma 💵 chance igual de roleta (vermelho-preto, par-ímpar), por exemplo, no "vermelho": fazemos uma aposta na roleta por 1 dólar; se você 💵 perder, dobramos e apostamos $ 2.
Se perdermos na roleta, perderemos a aposta atual ($ 2) e a aposta anterior ($ 💵 1) de $ 3.4, por exemplo.
duas apostas ganham (1 + 2 = $ 3) e temos um ganho líquido de 💵 $ 1 na roleta.
Se você perder uma segunda vez na roleta Martingale, dobramos a aposta novamente (agora é $ 4).
Se 💵 ganharmos, ganharemos de volta as duas apostas anteriores (1 + 2 = 3 dólares) e a atual (4 dólares) da 💵 roda da roleta, e novamente ganharemos 1 dólar do cassino [2].
Originalmente, a expressão "martingale" se referia a um grupo de 💵 estratégias de aposta popular na França do século XVIII.
[3][4] A mais simples destas estratégias foi projetada para um jogo betganha 💵 que o apostador ganhava se a moeda desse cara e perdia se a moeda desse coroa.
A estratégia fazia o apostador 💵 dobrar betganha aposta depois de cada derrota a fim de que a primeira vitória recuperasse todas as perdas anteriores, além 💵 de um lucro igual à primeira aposta.
Conforme o dinheiro e o tempo disponível do apostador se aproximam conjuntamente do infinito, 💵 a possibilidade de eventualmente dar cara se aproxima de 1, o que faz a estratégia de aposta martingale parecer como 💵 algo certo.
Entretanto, o crescimento exponencial das apostas eventualmente leva os apostadores à falência, assumindo de forma óbvia e realista que 💵 a quantidade de dinheiro do apostador é finita (uma das razões pelas quais casinos, ainda que desfrutem normativamente de uma 💵 vantagem matemática nos jogos oferecidos aos seus clientes, impõem limites às apostas).
Um movimento browniano parado, que é um processo martingale, 💵 pode ser usado para descrever a trajetória de tais jogos.
O conceito de martingale betganha teoria das probabilidades foi introduzido por 💵 Paul Lévy betganha 1934, ainda que ele não lhes tivesse dado este nome.
[5] O termo "martingale" foi introduzido betganha 1939 💵 por Jean Ville,[6] que também estendeu a definição à martingales contínuos.
[7] Muito do desenvolvimento original da teoria foi feito por 💵 Joseph Leo Doob, entre outros.
[8] Parte da motivação daquele trabalho era mostrar a impossibilidade de estratégias de aposta bem-sucedidas.[9]
Uma definição 💵 básica de um martingale de tempo discreto diz que ele é um processo estocástico (isto é, uma sequência de variáveis 💵 aleatórias) X 1 , X 2 , X 3 , ...
{\displaystyle X_{1},X_{2},X_{3},...
} de tempo discreto que satisfaz, para qualquer tempo 💵 n {\displaystyle n} ,
E ( | X n | ) < ∞ {\displaystyle \mathbf {E} (\vert X_{n}\vert )<\infty }
E ( 💵 X n + 1 ∣ X 1 , .
.
.
, X n ) = X n .
{\displaystyle \mathbf {E} (X_{n+1}\mid 💵 X_{1},\ldots ,X_{n})=X_{n}.}
Isto é, o valor esperado condicional da próxima observação, dadas todas as observações anteriores, é igual à mais recente 💵 observação.[10]
Sequências martingale betganha relação a outra sequência [ editar | editar código-fonte ]
Mais geralmente, uma sequência Y 1 , Y 💵 2 , Y 3 , ...
{\displaystyle Y_{1},Y_{2},Y_{3},...
} é considerada um martingale betganha relação a outra sequência X 1 , X 💵 2 , X 3 , ...
{\displaystyle X_{1},X_{2},X_{3},...
} se, para todo n {\displaystyle n} ,
E ( | Y n | ) 💵 < ∞ {\displaystyle \mathbf {E} (\vert Y_{n}\vert )<\infty }
E ( Y n + 1 ∣ X 1 , .
.
.
, 💵 X n ) = Y n .
{\displaystyle \mathbf {E} (Y_{n+1}\mid X_{1},\ldots ,X_{n})=Y_{n}.}
Da mesma forma, um martingale de tempo contínuo betganha 💵 relação ao processo estocástico X t {\displaystyle X_{t}} é um processo estocástico Y t {\displaystyle Y_{t}} tal que, para todo 💵 t {\displaystyle t} ,
E ( | Y t | ) < ∞ {\displaystyle \mathbf {E} (\vert Y_{t}\vert )<\infty }
E ( 💵 Y t ∣ { X τ , τ ≤ s } ) = Y s ∀ s ≤ t .
{\displaystyle 💵 \mathbf {E} (Y_{t}\mid \{X_{\tau },\tau \leq s\})=Y_{s}\quad \forall s\leq t.}
Isto expressa a propriedade de que o valor esperado condicional de 💵 qualquer observação no tempo t {\displaystyle t} , dadas todas as observações até o tempo s {\displaystyle s} , é 💵 igual à observação no tempo s {\displaystyle s} (considerando que s ≤ t {\displaystyle s\leq t} ).
Em geral, um processo 💵 estocástico Y : T × Ω → S {\displaystyle Y:T\times \Omega \to S} é um martingale betganha relação a uma 💵 filtração Σ ∗ {\displaystyle \Sigma _{*}} e medida de probabilidade P {\displaystyle P} se
Σ ∗ {\displaystyle \Sigma _{*}} espaço de 💵 probabilidade subjacente ( Ω , Σ , P {\displaystyle \Omega ,\Sigma ,P}
espaço de probabilidade subjacente ( Y {\displaystyle Y} Σ 💵 ∗ {\displaystyle \Sigma _{*}} t {\displaystyle t} T {\displaystyle T} Y t {\displaystyle Y_{t}} função mensurável Σ τ {\displaystyle \Sigma 💵 _{\tau }}
função mensurável Para cada t {\displaystyle t} Y t {\displaystyle Y_{t}} espaço Lp L 1 ( Ω , Σ 💵 t , P ; S ) {\displaystyle L^{1}(\Omega ,\Sigma _{t},P;S)}
E P ( | Y t | ) < + ∞ 💵 ; {\displaystyle \mathbf {E} _{\mathbf {P} }(|Y_{t}|)<+\infty ;}
Para todo s {\displaystyle s} t {\displaystyle t} s < t {\displaystyle s E P ( [ Y t − Y s ] χ F ) 💵 = 0 , {\displaystyle \mathbf {E} _{\mathbf {P} }\left([Y_{t}-Y_{s}]\chi _{F}\right)=0,} betganha que χ F {\displaystyle \chi _{F}} função indicadora do 💵 evento F {\displaystyle F} A última condição é denotada como Y s = E P ( Y t | Σ 💵 s ) , {\displaystyle Y_{s}=\mathbf {E} _{\mathbf {P} }(Y_{t}|\Sigma _{s}),} que é uma forma geral de valor esperado condicional.[ 11 💵 ] É importante notar que a propriedade martingale envolve tanto a filtração, como a medida de probabilidade (em relação à qual 💵 os valores esperados são assumidos). É possível que Y {\displaystyle Y} seja um martingale betganha relação a uma medida, mas não 💵 betganha relação a outra. O Teorema de Girsanov oferece uma forma de encontrar uma medida betganha relação à qual um processo 💵 de Itō é um martingale.[12] Exemplos de martingales [ editar | editar código-fonte ] Um passeio aleatório não viesado (em qualquer número 💵 de dimensões) é um exemplo de martingale. O dinheiro de um apostador é um martingale se todos os jogos de aposta 💵 com que ele se envolver forem honestos. Uma urna de Pólya contém uma quantidade de bolas de diferentes cores. A cada iteração, 💵 uma bola é aleatoriamente retirada da urna e substituída por várias outras da mesma cor. Para qualquer cor dada, a fração 💵 das bolas na urna com aquela cor é um martingale. Por exemplo, se atualmente 95% da bolas são vermelhas, então, ainda 💵 que a próxima iteração mais provavelmente adicione bolas vermelhas e não de outra cor, este viés está exatamente equilibrado pelo 💵 fato de que adicionar mais bolas vermelhas altera a fração de forma muito menos significativa do que adicionar o mesmo 💵 número de bolas não vermelhas alteraria. Suponha que X n {\displaystyle X_{n}} moeda honesta foi jogada n {\displaystyle n} moeda honesta foi 💵 jogada Considere Y n = X n 2 − n {\displaystyle Y_{n}={X_{n}}^{2}-n} X n {\displaystyle X_{n}} { Y n : 💵 n = 1 , 2 , 3 , ... } {\displaystyle \{Y_{n}:n=1,2,3,... \}} raiz quadrada do número de vezes que a moeda 💵 for jogada. raiz quadrada do número de vezes que a moeda for jogada. No caso de um martingale de Moivre, suponha que 💵 a moeda é desonesta, isto é, viesada, com probabilidade p {\displaystyle p} q = 1 − p {\displaystyle q=1-p} X n 💵 + 1 = X n ± 1 {\displaystyle X_{n+1}=X_{n}\pm 1} com + {\displaystyle +} − {\displaystyle -} Y n = ( 💵 q / p ) X n . {\displaystyle Y_{n}=(q/p)^{X_{n}}.} Então, { Y n : n = 1 , 2 , 3 , 💵 ... } {\displaystyle \{Y_{n}:n=1,2,3,... \}} { X n : n = 1 , 2 , 3 , ... } {\displaystyle \{X_{n}:n=1,2,3,... \}} E [ 💵 Y n + 1 ∣ X 1 , . . . , X n ] = p ( q / p ) 💵 X n + 1 + q ( q / p ) X n − 1 = p ( q / 💵 p ) ( q / p ) X n + q ( p / q ) ( q / p 💵 ) X n = q ( q / p ) X n + p ( q / p ) X 💵 n = ( q / p ) X n = Y n . {\displaystyle {\begin{aligned}E[Y_{n+1}\mid X_{1},\dots ,X_{n}]&=p(q/p)^{X_{n}+1}+q(q/p)^{X_{n}-1}\\[6pt]&=p(q/p)(q/p)^{X_{n}}+q(p/q)(q/p)^{X_{n}}\\[6pt]&=q(q/p)^{X_{n}}+p(q/p)^{X_{n}}=(q/p)^{X_{n}}=Y_{n}.\end{aligned}}} No teste de razão de 💵 verossimilhança betganha estatística, uma variável aleatória X {\displaystyle X} f {\displaystyle f} g {\displaystyle g} amostra aleatória X 1 , 💵 ... , X n {\displaystyle X_{1},... ,X_{n}} [ 13 ] Considere Y n {\displaystyle Y_{n}} Y n = ∏ i = 1 n 💵 g ( X i ) f ( X i ) {\displaystyle Y_{n}=\prod _{i=1}^{n}{\frac {g(X_{i})}{f(X_{i})}}} Se X {\displaystyle X} f {\displaystyle f} 💵 g {\displaystyle g} { Y n : n = 1 , 2 , 3 , ... } {\displaystyle \{Y_{n}:n=1,2,3,... \}} { X 💵 n : n = 1 , 2 , 3 , ... } {\displaystyle \{X_{n}:n=1,2,3,...\}} Suponha que uma ameba se divide betganha duas 💵 amebas com probabilidade p {\displaystyle p} 1 − p {\displaystyle 1-p} X n {\displaystyle X_{n}} n {\displaystyle n} X n 💵 = 0 {\displaystyle X_{n}=0} r {\displaystyle r} r {\displaystyle r} p {\displaystyle p} [ 14 ] Então { r X n 💵 : n = 1 , 2 , 3 , . . . } {\displaystyle \{\,r^{X_{n}}:n=1,2,3,\dots \,\}} é um martingale betganha relação a { 💵 X n : n = 1 , 2 , 3 , ... } {\displaystyle \{X_{n}:n=1,2,3,...\}} Uma série martingale criada por software. Em uma 💵 comunidade ecológica (um grupo de espécies betganha um nível trófico particular, competindo por recursos semelhantes betganha uma área local), o 💵 número de indivíduos de qualquer espécie particular de tamanho fixado é uma função de tempo (discreto) e pode ser visto 💵 como uma sequência de variáveis aleatórias. Esta sequência é um martingale sob a teoria neutra unificada de biodiversidade e biogeografia. Se { 💵 N t : t ≥ 0 } {\displaystyle \{N_{t}:t\geq 0\}} processo de Poisson com intensidade λ {\displaystyle \lambda } { 💵 N t − λ t : t ≥ 0 } {\displaystyle \{N_{t}-\lambda _{t}:t\geq 0\}} Submartingales, supermartingales e relação com funções harmônicas 💵 [ editar | editar código-fonte ] Há duas generalizações populares de um martingale que também incluem casos betganha que a observação 💵 atual X n {\displaystyle X_{n}} não é necessariamente igual à futura expectativa condicional E [ X n + 1 | 💵 X 1 , ... , X n ] {\displaystyle E[X_{n+1}|X_{1},... ,X_{n}]} , mas, betganha vez disto, a um limite superior ou inferior 💵 à expectativa condicional. Estas definições refletem uma relação entre a teoria do martingale e a teoria do potencial, que é o 💵 estudo das funções harmônicas. [15] Assim como um martingale de tempo contínuo satisfaz a E [ X t | { X 💵 τ : τ ≤ s } − X s = 0 ∀ s ≤ t {\displaystyle E[X_{t}|\{X_{\tau }:\tau \leq s\}-X_{s}=0\forall 💵 s\leq t} , uma função harmônica f {\displaystyle f} satisfaz a equação diferencial parcial Δ f = 0 {\displaystyle \Delta 💵 f=0} , betganha que Δ {\displaystyle \Delta } é o operador de Laplace. Dado um processo de movimento browniano W t 💵 {\displaystyle W_{t}} e uma função harmônica f {\displaystyle f} , o processo resultante f ( W t ) {\displaystyle f(W_{t})} 💵 também é um martingale. Um submartingale de tempo discreto é uma sequência X 1 , X 2 , X 3 , 💵 . . . {\displaystyle X_{1},X_{2},X_{3},\ldots } integráveis que satisfaz a E [ X n + 1 | X 1 , . . . , X 💵 n ] ≥ X n . {\displaystyle {}E[X_{n+1}|X_{1},\ldots ,X_{n}]\geq X_{n}. } Da mesma forma, um submartingale de tempo contínuo satisfaz a E 💵 [ X t | { X τ : τ ≤ s } ] ≥ X s ∀ s ≤ t 💵 . {\displaystyle {}E[X_{t}|\{X_{\tau }:\tau \leq s\}]\geq X_{s}\quad \forall s\leq t. } Em teoria do potencial, uma função sub-harmônica f {\displaystyle f} Δ 💵 f ≥ 0 {\displaystyle \Delta f\geq 0} Grosso modo, o prefixo "sub-" é consistente porque a atual observação X n 💵 {\displaystyle X_{n}} E [ X n + 1 | X 1 , ... , X n ] {\displaystyle E[X_{n+1}|X_{1},...,X_{n}]} De forma análoga, 💵 um supermartingale de tempo discreto satisfaz a E [ X n + 1 | X 1 , . . . , X n 💵 ] ≤ X n . {\displaystyle {}E[X_{n+1}|X_{1},\ldots ,X_{n}]\leq X_{n}. } Da mesma forma, um supermartingale de tempo contínuo satisfaz a E [ 💵 X t | { X τ : τ ≤ s } ] ≤ X s ∀ s ≤ t . {\displaystyle 💵 {}E[X_{t}|\{X_{\tau }:\tau \leq s\}]\leq X_{s}\quad \forall s\leq t. } Em teoria do potencial, uma função super-harmônica f {\displaystyle f} Δ f 💵 ≤ 0 {\displaystyle \Delta f\leq 0} Grosso modo, o prefixo "super-" é consistente porque a atual observação X n {\displaystyle 💵 X_{n}} E [ X n + 1 | X 1 , ... , X n ] {\displaystyle E[X_{n+1}|X_{1},...,X_{n}]} Exemplos de submartingales e 💵 supermartingales [ editar | editar código-fonte ] Todo martingale é também um submartingale e um supermartingale. Reciprocamente, todo processo estocástico que é 💵 tanto um submartingale, como um supermartingale, é um martingale. Considere novamente um apostador que ganha $1 quando uma moeda der cara 💵 e perde $1 quando a moeda der coroa. Suponha agora que a moeda possa estar viesada e que ela dê cara 💵 com probabilidade p {\displaystyle p} Se p {\displaystyle p} 1 / 2 {\displaystyle 1/2} Se p {\displaystyle p} 1 / 💵 2 {\displaystyle 1/2} Se p {\displaystyle p} 1 / 2 {\displaystyle 1/2} Uma função convexa de um martingale é um submartingale 💵 pela desigualdade de Jensen. Por exemplo, o quadrado da riqueza de um apostador betganha jogo de moeda honesta é um submartingale 💵 (o que também se segue do fato de que X n 2 − n {\displaystyle {X_{n}}^{2}-n} Martingales e tempos de parada 💵 [ editar | editar código-fonte ] Um tempo de parada betganha relação a uma sequência de variáveis aleatórias X 1 , 💵 X 2 , X 3 , ... {\displaystyle X_{1},X_{2},X_{3},... } é uma variável aleatória τ {\displaystyle \tau } com a propriedade de 💵 que para cada t {\displaystyle t} , a ocorrência ou a não ocorrência do evento τ = t {\displaystyle \tau 💵 =t} depende apenas dos valores de X 1 , X 2 , X 3 , ... , X t {\displaystyle X_{1},X_{2},X_{3},...,X_{t}} 💵 . A intuição por trás da definição é que, a qualquer tempo particular t {\displaystyle t} , pode-se observar a sequência 💵 até o momento e dizer se é hora de parar. Um exemplo na vida real pode ser o tempo betganha que 💵 um apostador deixa a mesa de apostas, o que pode ser uma função de suas vitórias anteriores (por exemplo, ele 💵 pode deixar a mesa apenas quando ele vai à falência), mas ele não pode escolher entre ficar ou sair com 💵 base no resultando de jogos que ainda não ocorreram.[16] Em alguns contextos, o conceito de tempo de parada é definido exigindo-se 💵 apenas que a ocorrência ou não ocorrência do evento τ = t {\displaystyle \tau =t} seja probabilisticamente independente de X 💵 t + 1 , X t + 2 , ... {\displaystyle X_{t+1},X_{t+2},... } , mas não que isto seja completamente determinado pelo 💵 histórico do processo até o tempo t {\displaystyle t} . Isto é uma condição mais fraca do que aquela descrita no 💵 parágrafo acima, mas é forte o bastante para servir betganha algumas das provas betganha que tempos de parada são usados. Uma 💵 das propriedades básicas de martingales é que, se ( X t ) t > 0 {\displaystyle (X_{t})_{t>0}} for um (sub/super)martingale 💵 e τ {\displaystyle \tau } for um tempo de parada, então, o processo parado correspondente ( X t τ ) 💵 t > 0 {\displaystyle (X_{t}^{\tau })_{t>0}} definido por X t τ := X min { τ , t } {\displaystyle 💵 X_{t}^{\tau }:=X_{\min\{\tau ,t\}}} é também um (sub/super) martingale. O conceito de um martingale parado leva a uma série de teoremas importantes, 💵 incluindo, por exemplo, o teorema da parada opcional, que afirma que, sob certas condições, o valor esperado de um martingale 💵 betganha um tempo de parada é igual ao seu valor inicial. Em teoria das probabilidades, um martingale é um modelo de 💵 jogo honesto (fair game) betganha que o conhecimento de eventos passados nunca ajuda a prever os ganhos futuros e apenas 💵 o evento atual importa. Em particular, um martingale é uma sequência de variáveis aleatórias (isto é, um processo estocástico) para o 💵 qual, a qualquer tempo específico na sequência observada, a esperança do próximo valor na sequência é igual ao valor presentemente 💵 observado, mesmo dado o conhecimento de todos os valores anteriormente observados.[1] O movimento browniano parado é um exemplo de martingale. Ele pode 💵 modelar um jogo de cara ou coroa com a possibilidade de falência. Em contraste, betganha um processo que não é um 💵 martingale, o valor esperado do processo betganha um tempo pode ainda ser igual ao valor esperado do processo no tempo 💵 seguinte. Entretanto, o conhecimento de eventos anteriores (por exemplo, todas as cartas anteriormente retiradas de um baralho) pode ajudar a reduzir 💵 a incerteza sobre os eventos futuros. Assim, o valor esperado do próximo evento, dado o conhecimento do evento presente e de 💵 todos os anteriores, pode ser mais elevado do que o do presente evento se uma estratégia de ganho for usada. Martingales 💵 excluem a possibilidade de estratégias de ganho baseadas no histórico do jogo e, portanto, são um modelo de jogos honestos. É 💵 também uma técnica utilizada no mercado financeiro, para recuperar operações perdidas. Dobra-se a segunda mão para recuperar a anterior, e assim 💵 sucessivamente, até o acerto. Martingale é o sistema de apostas mais comum na roleta. A popularidade deste sistema se deve à betganha 💵 simplicidade e acessibilidade. O jogo Martingale dá a impressão enganosa de vitórias rápidas e fáceis. A essência do sistema de jogo da 💵 roleta Martingale é a seguinte: fazemos uma aposta betganha uma chance igual de roleta (vermelho-preto, par-ímpar), por exemplo, no "vermelho": 💵 fazemos uma aposta na roleta por 1 dólar; se você perder, dobramos e apostamos $ 2. Se perdermos na roleta, perderemos 💵 a aposta atual ($ 2) e a aposta anterior ($ 1) de $ 3.4, por exemplo. duas apostas ganham (1 + 💵 2 = $ 3) e temos um ganho líquido de $ 1 na roleta. Se você perder uma segunda vez na 💵 roleta Martingale, dobramos a aposta novamente (agora é $ 4). Se ganharmos, ganharemos de volta as duas apostas anteriores (1 + 💵 2 = 3 dólares) e a atual (4 dólares) da roda da roleta, e novamente ganharemos 1 dólar do cassino 💵 [2]. Originalmente, a expressão "martingale" se referia a um grupo de estratégias de aposta popular na França do século XVIII. [3][4] A 💵 mais simples destas estratégias foi projetada para um jogo betganha que o apostador ganhava se a moeda desse cara e 💵 perdia se a moeda desse coroa. A estratégia fazia o apostador dobrar betganha aposta depois de cada derrota a fim de 💵 que a primeira vitória recuperasse todas as perdas anteriores, além de um lucro igual à primeira aposta. Conforme o dinheiro e 💵 o tempo disponível do apostador se aproximam conjuntamente do infinito, a possibilidade de eventualmente dar cara se aproxima de 1, 💵 o que faz a estratégia de aposta martingale parecer como algo certo. Entretanto, o crescimento exponencial das apostas eventualmente leva os 💵 apostadores à falência, assumindo de forma óbvia e realista que a quantidade de dinheiro do apostador é finita (uma das 💵 razões pelas quais casinos, ainda que desfrutem normativamente de uma vantagem matemática nos jogos oferecidos aos seus clientes, impõem limites 💵 às apostas). Um movimento browniano parado, que é um processo martingale, pode ser usado para descrever a trajetória de tais jogos. O 💵 conceito de martingale betganha teoria das probabilidades foi introduzido por Paul Lévy betganha 1934, ainda que ele não lhes tivesse 💵 dado este nome. [5] O termo "martingale" foi introduzido betganha 1939 por Jean Ville,[6] que também estendeu a definição à martingales 💵 contínuos. [7] Muito do desenvolvimento original da teoria foi feito por Joseph Leo Doob, entre outros. [8] Parte da motivação daquele trabalho 💵 era mostrar a impossibilidade de estratégias de aposta bem-sucedidas.[9] Uma definição básica de um martingale de tempo discreto diz que ele 💵 é um processo estocástico (isto é, uma sequência de variáveis aleatórias) X 1 , X 2 , X 3 , 💵 ... {\displaystyle X_{1},X_{2},X_{3},... } de tempo discreto que satisfaz, para qualquer tempo n {\displaystyle n} , E ( | X n | ) 💵 < ∞ {\displaystyle \mathbf {E} (\vert X_{n}\vert )<\infty } E ( X n + 1 ∣ X 1 , . . . , 💵 X n ) = X n . {\displaystyle \mathbf {E} (X_{n+1}\mid X_{1},\ldots ,X_{n})=X_{n}.} Isto é, o valor esperado condicional da próxima observação, 💵 dadas todas as observações anteriores, é igual à mais recente observação.[10] Sequências martingale betganha relação a outra sequência [ editar | 💵 editar código-fonte ] Mais geralmente, uma sequência Y 1 , Y 2 , Y 3 , ... {\displaystyle Y_{1},Y_{2},Y_{3},... } é considerada um 💵 martingale betganha relação a outra sequência X 1 , X 2 , X 3 , ... {\displaystyle X_{1},X_{2},X_{3},... } se, para todo 💵 n {\displaystyle n} , E ( | Y n | ) < ∞ {\displaystyle \mathbf {E} (\vert Y_{n}\vert )<\infty } E ( 💵 Y n + 1 ∣ X 1 , . . . , X n ) = Y n . {\displaystyle \mathbf {E} (Y_{n+1}\mid 💵 X_{1},\ldots ,X_{n})=Y_{n}.} Da mesma forma, um martingale de tempo contínuo betganha relação ao processo estocástico X t {\displaystyle X_{t}} é um 💵 processo estocástico Y t {\displaystyle Y_{t}} tal que, para todo t {\displaystyle t} , E ( | Y t | ) 💵 < ∞ {\displaystyle \mathbf {E} (\vert Y_{t}\vert )<\infty } E ( Y t ∣ { X τ , τ ≤ s 💵 } ) = Y s ∀ s ≤ t . {\displaystyle \mathbf {E} (Y_{t}\mid \{X_{\tau },\tau \leq s\})=Y_{s}\quad \forall s\leq t.} Isto 💵 expressa a propriedade de que o valor esperado condicional de qualquer observação no tempo t {\displaystyle t} , dadas todas 💵 as observações até o tempo s {\displaystyle s} , é igual à observação no tempo s {\displaystyle s} (considerando que 💵 s ≤ t {\displaystyle s\leq t} ). Em geral, um processo estocástico Y : T × Ω → S {\displaystyle Y:T\times 💵 \Omega \to S} é um martingale betganha relação a uma filtração Σ ∗ {\displaystyle \Sigma _{*}} e medida de probabilidade 💵 P {\displaystyle P} se Σ ∗ {\displaystyle \Sigma _{*}} espaço de probabilidade subjacente ( Ω , Σ , P {\displaystyle \Omega 💵 ,\Sigma ,P} espaço de probabilidade subjacente ( Y {\displaystyle Y} Σ ∗ {\displaystyle \Sigma _{*}} t {\displaystyle t} T {\displaystyle T} 💵 Y t {\displaystyle Y_{t}} função mensurável Σ τ {\displaystyle \Sigma _{\tau }} função mensurável Para cada t {\displaystyle t} Y t 💵 {\displaystyle Y_{t}} espaço Lp L 1 ( Ω , Σ t , P ; S ) {\displaystyle L^{1}(\Omega ,\Sigma _{t},P;S)} E 💵 P ( | Y t | ) < + ∞ ; {\displaystyle \mathbf {E} _{\mathbf {P} }(|Y_{t}|)<+\infty ;} Para todo s 💵 {\displaystyle s} t {\displaystyle t} s < t {\displaystyle s E P ( 💵 [ Y t − Y s ] χ F ) = 0 , {\displaystyle \mathbf {E} _{\mathbf {P} }\left([Y_{t}-Y_{s}]\chi _{F}\right)=0,} 💵 betganha que χ F {\displaystyle \chi _{F}} função indicadora do evento F {\displaystyle F} A última condição é denotada como 💵 Y s = E P ( Y t | Σ s ) , {\displaystyle Y_{s}=\mathbf {E} _{\mathbf {P} }(Y_{t}|\Sigma _{s}),} 💵 que é uma forma geral de valor esperado condicional.[ 11 ] É importante notar que a propriedade martingale envolve tanto a 💵 filtração, como a medida de probabilidade (em relação à qual os valores esperados são assumidos). É possível que Y {\displaystyle Y} 💵 seja um martingale betganha relação a uma medida, mas não betganha relação a outra. O Teorema de Girsanov oferece uma forma 💵 de encontrar uma medida betganha relação à qual um processo de Itō é um martingale.[12] Exemplos de martingales [ editar | 💵 editar código-fonte ] Um passeio aleatório não viesado (em qualquer número de dimensões) é um exemplo de martingale. O dinheiro de um 💵 apostador é um martingale se todos os jogos de aposta com que ele se envolver forem honestos. Uma urna de Pólya 💵 contém uma quantidade de bolas de diferentes cores. A cada iteração, uma bola é aleatoriamente retirada da urna e substituída por 💵 várias outras da mesma cor. Para qualquer cor dada, a fração das bolas na urna com aquela cor é um martingale. Por 💵 exemplo, se atualmente 95% da bolas são vermelhas, então, ainda que a próxima iteração mais provavelmente adicione bolas vermelhas e 💵 não de outra cor, este viés está exatamente equilibrado pelo fato de que adicionar mais bolas vermelhas altera a fração 💵 de forma muito menos significativa do que adicionar o mesmo número de bolas não vermelhas alteraria. Suponha que X n {\displaystyle 💵 X_{n}} moeda honesta foi jogada n {\displaystyle n} moeda honesta foi jogada Considere Y n = X n 2 − n 💵 {\displaystyle Y_{n}={X_{n}}^{2}-n} X n {\displaystyle X_{n}} { Y n : n = 1 , 2 , 3 , ... } {\displaystyle 💵 \{Y_{n}:n=1,2,3,... \}} raiz quadrada do número de vezes que a moeda for jogada. raiz quadrada do número de vezes que a moeda 💵 for jogada. No caso de um martingale de Moivre, suponha que a moeda é desonesta, isto é, viesada, com probabilidade p 💵 {\displaystyle p} q = 1 − p {\displaystyle q=1-p} X n + 1 = X n ± 1 {\displaystyle X_{n+1}=X_{n}\pm 1} 💵 com + {\displaystyle +} − {\displaystyle -} Y n = ( q / p ) X n . {\displaystyle Y_{n}=(q/p)^{X_{n}}.} Então, { Y 💵 n : n = 1 , 2 , 3 , ... } {\displaystyle \{Y_{n}:n=1,2,3,... \}} { X n : n = 1 💵 , 2 , 3 , ... } {\displaystyle \{X_{n}:n=1,2,3,... \}} E [ Y n + 1 ∣ X 1 , . . . , 💵 X n ] = p ( q / p ) X n + 1 + q ( q / p 💵 ) X n − 1 = p ( q / p ) ( q / p ) X n + 💵 q ( p / q ) ( q / p ) X n = q ( q / p ) 💵 X n + p ( q / p ) X n = ( q / p ) X n = 💵 Y n . {\displaystyle {\begin{aligned}E[Y_{n+1}\mid X_{1},\dots ,X_{n}]&=p(q/p)^{X_{n}+1}+q(q/p)^{X_{n}-1}\\[6pt]&=p(q/p)(q/p)^{X_{n}}+q(p/q)(q/p)^{X_{n}}\\[6pt]&=q(q/p)^{X_{n}}+p(q/p)^{X_{n}}=(q/p)^{X_{n}}=Y_{n}.\end{aligned}}} No teste de razão de verossimilhança betganha estatística, uma variável aleatória X {\displaystyle X} f 💵 {\displaystyle f} g {\displaystyle g} amostra aleatória X 1 , ... , X n {\displaystyle X_{1},... ,X_{n}} [ 13 ] Considere Y 💵 n {\displaystyle Y_{n}} Y n = ∏ i = 1 n g ( X i ) f ( X i ) 💵 {\displaystyle Y_{n}=\prod _{i=1}^{n}{\frac {g(X_{i})}{f(X_{i})}}} Se X {\displaystyle X} f {\displaystyle f} g {\displaystyle g} { Y n : n = 1 💵 , 2 , 3 , ... } {\displaystyle \{Y_{n}:n=1,2,3,... \}} { X n : n = 1 , 2 , 3 , 💵 ... } {\displaystyle \{X_{n}:n=1,2,3,...\}} Suponha que uma ameba se divide betganha duas amebas com probabilidade p {\displaystyle p} 1 − p {\displaystyle 💵 1-p} X n {\displaystyle X_{n}} n {\displaystyle n} X n = 0 {\displaystyle X_{n}=0} r {\displaystyle r} r {\displaystyle r} 💵 p {\displaystyle p} [ 14 ] Então { r X n : n = 1 , 2 , 3 , . . . 💵 } {\displaystyle \{\,r^{X_{n}}:n=1,2,3,\dots \,\}} é um martingale betganha relação a { X n : n = 1 , 2 , 3 💵 , ... } {\displaystyle \{X_{n}:n=1,2,3,...\}} Uma série martingale criada por software. Em uma comunidade ecológica (um grupo de espécies betganha um nível trófico 💵 particular, competindo por recursos semelhantes betganha uma área local), o número de indivíduos de qualquer espécie particular de tamanho fixado 💵 é uma função de tempo (discreto) e pode ser visto como uma sequência de variáveis aleatórias. Esta sequência é um martingale 💵 sob a teoria neutra unificada de biodiversidade e biogeografia. Se { N t : t ≥ 0 } {\displaystyle \{N_{t}:t\geq 0\}} 💵 processo de Poisson com intensidade λ {\displaystyle \lambda } { N t − λ t : t ≥ 0 } 💵 {\displaystyle \{N_{t}-\lambda _{t}:t\geq 0\}} Submartingales, supermartingales e relação com funções harmônicas [ editar | editar código-fonte ] Há duas generalizações populares de 💵 um martingale que também incluem casos betganha que a observação atual X n {\displaystyle X_{n}} não é necessariamente igual à 💵 futura expectativa condicional E [ X n + 1 | X 1 , ... , X n ] {\displaystyle E[X_{n+1}|X_{1},... ,X_{n}]} , 💵 mas, betganha vez disto, a um limite superior ou inferior à expectativa condicional. Estas definições refletem uma relação entre a teoria 💵 do martingale e a teoria do potencial, que é o estudo das funções harmônicas. [15] Assim como um martingale de tempo 💵 contínuo satisfaz a E [ X t | { X τ : τ ≤ s } − X s = 💵 0 ∀ s ≤ t {\displaystyle E[X_{t}|\{X_{\tau }:\tau \leq s\}-X_{s}=0\forall s\leq t} , uma função harmônica f {\displaystyle f} satisfaz 💵 a equação diferencial parcial Δ f = 0 {\displaystyle \Delta f=0} , betganha que Δ {\displaystyle \Delta } é o 💵 operador de Laplace. Dado um processo de movimento browniano W t {\displaystyle W_{t}} e uma função harmônica f {\displaystyle f} , 💵 o processo resultante f ( W t ) {\displaystyle f(W_{t})} também é um martingale. Um submartingale de tempo discreto é uma 💵 sequência X 1 , X 2 , X 3 , . . . {\displaystyle X_{1},X_{2},X_{3},\ldots } integráveis que satisfaz a E [ X 💵 n + 1 | X 1 , . . . , X n ] ≥ X n . {\displaystyle {}E[X_{n+1}|X_{1},\ldots ,X_{n}]\geq X_{n}. } Da 💵 mesma forma, um submartingale de tempo contínuo satisfaz a E [ X t | { X τ : τ ≤ 💵 s } ] ≥ X s ∀ s ≤ t . {\displaystyle {}E[X_{t}|\{X_{\tau }:\tau \leq s\}]\geq X_{s}\quad \forall s\leq t. } Em 💵 teoria do potencial, uma função sub-harmônica f {\displaystyle f} Δ f ≥ 0 {\displaystyle \Delta f\geq 0} Grosso modo, o 💵 prefixo "sub-" é consistente porque a atual observação X n {\displaystyle X_{n}} E [ X n + 1 | X 💵 1 , ... , X n ] {\displaystyle E[X_{n+1}|X_{1},...,X_{n}]} De forma análoga, um supermartingale de tempo discreto satisfaz a E [ X n 💵 + 1 | X 1 , . . . , X n ] ≤ X n . {\displaystyle {}E[X_{n+1}|X_{1},\ldots ,X_{n}]\leq X_{n}. } Da mesma 💵 forma, um supermartingale de tempo contínuo satisfaz a E [ X t | { X τ : τ ≤ s 💵 } ] ≤ X s ∀ s ≤ t . {\displaystyle {}E[X_{t}|\{X_{\tau }:\tau \leq s\}]\leq X_{s}\quad \forall s\leq t. } Em teoria 💵 do potencial, uma função super-harmônica f {\displaystyle f} Δ f ≤ 0 {\displaystyle \Delta f\leq 0} Grosso modo, o prefixo 💵 "super-" é consistente porque a atual observação X n {\displaystyle X_{n}} E [ X n + 1 | X 1 💵 , ... , X n ] {\displaystyle E[X_{n+1}|X_{1},...,X_{n}]} Exemplos de submartingales e supermartingales [ editar | editar código-fonte ] Todo martingale é também 💵 um submartingale e um supermartingale. Reciprocamente, todo processo estocástico que é tanto um submartingale, como um supermartingale, é um martingale. Considere novamente 💵 um apostador que ganha $1 quando uma moeda der cara e perde $1 quando a moeda der coroa. Suponha agora que 💵 a moeda possa estar viesada e que ela dê cara com probabilidade p {\displaystyle p} Se p {\displaystyle p} 1 💵 / 2 {\displaystyle 1/2} Se p {\displaystyle p} 1 / 2 {\displaystyle 1/2} Se p {\displaystyle p} 1 / 2 💵 {\displaystyle 1/2} Uma função convexa de um martingale é um submartingale pela desigualdade de Jensen. Por exemplo, o quadrado da riqueza de 💵 um apostador betganha jogo de moeda honesta é um submartingale (o que também se segue do fato de que X 💵 n 2 − n {\displaystyle {X_{n}}^{2}-n} Martingales e tempos de parada [ editar | editar código-fonte ] Um tempo de parada betganha 💵 relação a uma sequência de variáveis aleatórias X 1 , X 2 , X 3 , ... {\displaystyle X_{1},X_{2},X_{3},... } é uma 💵 variável aleatória τ {\displaystyle \tau } com a propriedade de que para cada t {\displaystyle t} , a ocorrência ou 💵 a não ocorrência do evento τ = t {\displaystyle \tau =t} depende apenas dos valores de X 1 , X 💵 2 , X 3 , ... , X t {\displaystyle X_{1},X_{2},X_{3},...,X_{t}} . A intuição por trás da definição é que, a qualquer 💵 tempo particular t {\displaystyle t} , pode-se observar a sequência até o momento e dizer se é hora de parar. Um 💵 exemplo na vida real pode ser o tempo betganha que um apostador deixa a mesa de apostas, o que pode 💵 ser uma função de suas vitórias anteriores (por exemplo, ele pode deixar a mesa apenas quando ele vai à falência), 💵 mas ele não pode escolher entre ficar ou sair com base no resultando de jogos que ainda não ocorreram.[16] Em alguns 💵 contextos, o conceito de tempo de parada é definido exigindo-se apenas que a ocorrência ou não ocorrência do evento τ 💵 = t {\displaystyle \tau =t} seja probabilisticamente independente de X t + 1 , X t + 2 , ... {\displaystyle 💵 X_{t+1},X_{t+2},... } , mas não que isto seja completamente determinado pelo histórico do processo até o tempo t {\displaystyle t} . Isto 💵 é uma condição mais fraca do que aquela descrita no parágrafo acima, mas é forte o bastante para servir betganha 💵 algumas das provas betganha que tempos de parada são usados. Uma das propriedades básicas de martingales é que, se ( X 💵 t ) t > 0 {\displaystyle (X_{t})_{t>0}} for um (sub/super)martingale e τ {\displaystyle \tau } for um tempo de parada, 💵 então, o processo parado correspondente ( X t τ ) t > 0 {\displaystyle (X_{t}^{\tau })_{t>0}} definido por X t 💵 τ := X min { τ , t } {\displaystyle X_{t}^{\tau }:=X_{\min\{\tau ,t\}}} é também um (sub/super) martingale. O conceito de 💵 um martingale parado leva a uma série de teoremas importantes, incluindo, por exemplo, o teorema da parada opcional, que afirma 💵 que, sob certas condições, o valor esperado de um martingale betganha um tempo de parada é igual ao seu valor 💵 inicial. No mundo de hoje, ganhar um dinheiro extra é cada vez mais importante e, novamente, a tecnologia nos ajuda a 🌞 faciliatar as coisas. Existem vários aplicativos disponíveis para serem baixados betganha betganha suas smartphones, que lhe ajudarão a GANHAR DINHEIRO. 🌞 Sim, ouvi bem, GANHAR DINHEIRO! Veja abaixo os 7 apps que recomendamos e que realmente pagam. 1. TikTok TikTok é uma rede 🌞 social extremamente popular, especialmente entre os jovens. Mas você sabe que também pode SER UMA FERREA PARA GANHAR DINHEIRO? Isso 🌞 mesmo, existem diversas marcas e empresas que procuram 'tiktokers' influentes para fazerem parcerias e divulgações de produtos ou serviços. Então, se 🌞 você tem um alto número de seguidores e engajamento betganha betganha betganha conta TikTok, porque não tentar monetizá-la? Você pode 🌞 estar se perguntando como? Bem, há diferentes formas de se fazer isto, como gerar conteúdo patrocinado, participar de desafios de 🌞 marcas, entre outras. 2. Kwai No evento KFC 50, A.J. Styles e Justin Edwards foram as primeiras colocadas, e no programa "Invincible", Styles fez uma breve 0️⃣ aparição, revelando que era betganha intenção de formar dupla com Edwards e os dois ganharam o torneio anual. Na edição anterior, 0️⃣ os dois receberam a medalha de prata, mas betganha performance não aumentou. Em 16 de Julho, foram confirmadas os membros da 0️⃣ A.J. Styles no Draft Extra da Liga pela NBA.como ganhar dinheiro na casa de aposta

como ganhar dinheiro na esporte da sorte
como ganhar dinheiro na estrela bet
guida, deposite fundos betganha betganha betganha conta através de um método de pagamento aceito.
ha o jogo de slots que você 🍏 deseja jogar, inicie-o e defina o tamanho da aposta. Agora,
você só precisa pressionar o botão de rotação para jogar uma 🍏 rodada. Como jogar as
s de apostas on-line e o guia do iniciante - Techopedia techopédia : guias de jogos
...
Seja bem-vindo ao bet365, o melhor site de apostas esportivas do mundo. Aqui você encontra as melhores opções de apostas, 4️⃣ com os melhores preços e as melhores promoções.
O bet365 oferece uma ampla gama de produtos de apostas esportivas, incluindo futebol, 4️⃣ basquete, tênis, vôlei e muito mais. Você pode apostar betganha betganha partidas ao vivo ou betganha betganha eventos futuros, e 4️⃣ ainda pode criar suas próprias apostas personalizadas.Além das apostas esportivas, o bet365 também oferece outros produtos, como jogos de cassino, 4️⃣ pôquer e bingo. Tudo isso betganha betganha um ambiente seguro e confiável, com atendimento ao cliente 24 horas por dia, 4️⃣ 7 dias por semana.
pergunta: Quais são os melhores produtos de apostas esportivas do bet365?
resposta: O bet365 oferece uma ampla gama 4️⃣ de produtos de apostas esportivas, incluindo futebol, basquete, tênis, vôlei e muito mais.
pergunta: Posso apostar betganha betganha partidas ao vivo 4️⃣ no bet365?